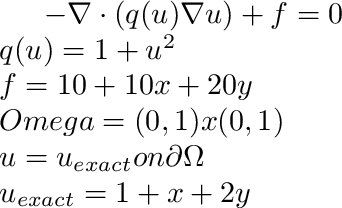#include "adh.h"

Functions
int	poisson_residual (SMODEL_SUPER mod, double elem_rhs, int ie, double perturbation, int perturb_node, int perturb_var, int perturb_sign, int DEBUG)
	Returns the 2D Poisson residual (linear or nonlinear), used for testing. More...

Detailed Description

This file collections functions responsible for the 2D Poisson equation with constant RHS, used for testing and 2D nonlinear Poisson equation for testing

Function Documentation

◆ poisson_residual()

int poisson_residual	(	SMODEL_SUPER *	mod,
		double *	elem_rhs,
		int	ie,
		double	perturbation,
		int	perturb_node,
		int	perturb_var,
		int	perturb_sign,
		int	DEBUG
	)

Returns the 2D Poisson residual (linear or nonlinear), used for testing.

Author: Charlie Berger, Ph.D.; Gaurav Savant, Ph.D.; Gary Brown; Corey Trahan, Ph.D.; Mark Loveland, Ph.D.

Bug:: none

Warning: none

Copyright: AdH

Parameters

[in]	mod	(SMODEL_SUPER*) - pointer to SMODEL_SUPER struct
[in,out]	elem_rhs	(double*) - array of doubles that will store elemental residual
[in]	ie	(int) - the elemental id
[in]	pertubation	(double) - the Newton pertubation
[in]	perturb_node	(int) - the node to be pertubed
[in]	perturb_var	(int) - the variable code to be perturbed
[in]	perturb_sign	(int) - the direction of Newton perturbation (-1 or +1)
[in]	DEBUG	(int) - a debug flag

Returns: integer code

If mod->LINEAR then solves the body integals of the following weak, discrete body terms of the 2D Poisson equation:
$\int_{\Omega} \nabla u_i \cdot \nabla v_i dx + \int_{\Omega} f dx = 0 \\ f=6 u_{exact} = 1 + x^2 + 2y^2\\$ If it is nonlinear then solves: $-\nabla \cdot (q(u) \nabla u) + f = 0\\ q(u) = 1 + u^2\\ f = 10 + 10x + 20y\\ Omega = (0,1) x (0,1)\\ u = u_{exact} on \partial \Omega\\ u_{exact} = 1 + x + 2y \\$

Functions

Detailed Description

Function Documentation

◆ poisson_residual()