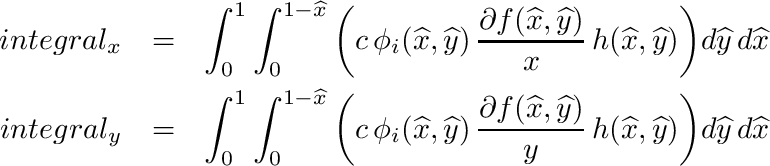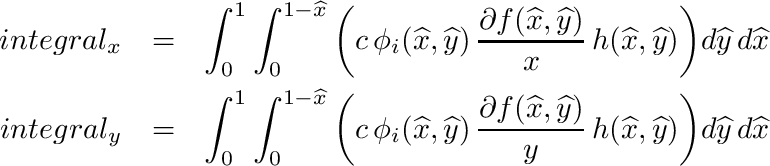|
|
void | extractNodesQuad (SVECT *v, double *x1, double *x2, double *x3, double *x4, double *y1, double *y2, double *y3, double *y4) |
| |
|
void | extractVect2DQuad (SVECT2D *v, double *x1, double *x2, double *x3, double *x4, double *y1, double *y2, double *y3, double *y4) |
| |
|
void | extractFunctionQuad (double *f, double *f1, double *f2, double *f3, double *f4) |
| |
| double | integrate_triangle_f (double djac, double c, double *f) |
| | Peforms following triangular integration: 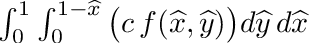 . More... . More...
|
| |
| double | integrate_triangle_f_f (double djac, double c, double *f) |
| | Peforms following triangular integration: 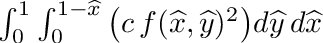 . More... . More...
|
| |
| void | integrate_triangle_phi_f (double djac, double c, double *f, double *integral) |
| | Peforms following triangular integration: 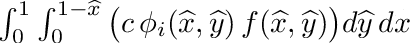 . More... . More...
|
| |
| void | integrate_triangle_phi_f_lump (double djac, double c, double *f, double *integral) |
| | Peforms following *lumped triangular integration: 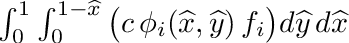 . More... . More...
|
| |
| void | integrate_triangle_gradPhi_dot_vbar (SVECT2D *grad_shp, double djac, double c, SVECT2D vbar, double *integral) |
| | Peforms following triangular integration: 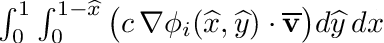 . More... . More...
|
| |
| void | integrate_triangle_phi_h_g_df (double djac, double c, double *h, double *g, SVECT2D df, double *integral_x, double *integral_y) |
| | Peforms following triangular integration: More...
|
| |
| void | grad2d_phi_f (SVECT2D *grad_phi, double *f, SVECT2D *grad, int ndof) |
| | Calculates 2D grad(phi) times a function. More...
|
| |
| void | grad2d_phi_dot_v (SVECT2D *grad_phi, SVECT2D *v, SVECT2D *grad_x, SVECT2D *grad_y, int ndof) |
| | Calculates grad(phi) times a 2D vector. More...
|
| |
| void | integrate_triangle_gradPhi_dot_v (SVECT2D *grad_shp, double djac, double c, SVECT2D *v, double *integral) |
| | Peforms following triangular integration: 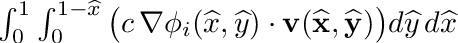 . More... . More...
|
| |
| double | integrate_quadrilateral_area (SVECT *nd, double c) |
| | Peforms following triangular integration: 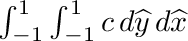 . More... . More...
|
| |
| double | integrate_quadrilateral_f (SVECT *nd, double c, double *f) |
| | Peforms following quadrilateral integration: 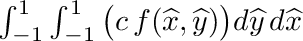 . More... . More...
|
| |
| SVECT2D | integrate_quadrilateral_gradF (SVECT *nd, double c, double *f) |
| | Peforms following quadrilateral integration: More...
|
| |
| void | integrate_triangle_gradPhi_dot_f_v (SVECT2D *grad_shp, double djac, double c, double *f, SVECT2D *v, double *integral) |
| | Peforms following triangular integration: 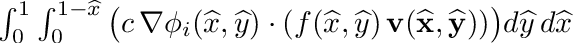 . More... . More...
|
| |
| void | integrate_triangle_gradPhi_dot_f_g_v (SVECT2D *grad_shp, double djac, double c, double *f, double *g, SVECT2D *v, double *integral) |
| | Peforms following triangular integration: 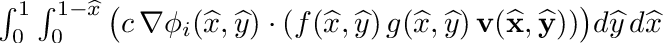 . More... . More...
|
| |
| void | integrate_triangle_dphi_f_g_h (SVECT2D *grad_shp, double djac, double c, double *f, double *g, double *h, double *integral_x, double *integral_y) |
| | Peforms following triangular integration: More...
|
| |
| void | integrate_triangle_dphi_f_f_h (SVECT2D *grad_shp, double djac, double c, double *f, double *h, double *integral_x, double *integral_y) |
| | Peforms following EITHER triangular integration: More...
|
| |
| void | integrate_triangle_phi (double djac, double c, double *integral) |
| | Peforms following triangular integration: 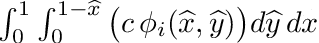 . More... . More...
|
| |
| void | integrate_triangle_dphi_f_f (SVECT2D *grad_shp, double djac, double c, double *f, double *integral_x, double *integral_y) |
| | Peforms following triangular integration: More...
|
| |
| void | integrate_triangle_phi_h_df (double djac, double c, double *h, SVECT2D df, double *integral_x, double *integral_y) |
| | Peforms following triangular integration: More...
|
| |
| void | integrate_triangle_phi_f_g (double djac, double c, double *f, double *g, double *integral) |
| | Peforms following triangular integration: 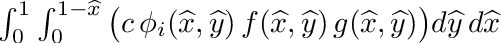 . More... . More...
|
| |
| void | integrate_quadrilateral_gradPhi_dot_f_v (SVECT *nd, double c, double *f, SVECT2D *v, double *integral) |
| | Peforms following quadrilateral integration: 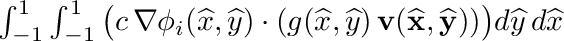 . More... . More...
|
| |
| void | integrate_quadrilateral_gradPhi_dot_f_g_v (SVECT *nd, double c, double *f, double *g, SVECT2D *v, double *integral) |
| | Peforms following quadrilateral integration: 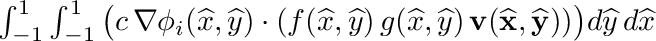 . More... . More...
|
| |
| void | integrate_quadrilateral_phi_f (SVECT *nd, double c, double *f, double *integral) |
| | Peforms following quadrilateral integration: 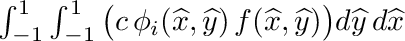 . More... . More...
|
| |
| void | integrate_quadrilateral_phi (SVECT *nd, double c, double *integral) |
| | Peforms following quadrilateral integration: 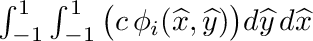 . More... . More...
|
| |
| void | integrate_quadrilateral_phi_f_lump (SVECT *nd, double c, double *f, double *integral) |
| | Peforms following *lumped quadrilateral integration: 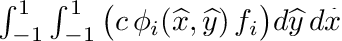 . More... . More...
|
| |
|
double | get_quadrilateral_linear_djac2d (double xhat, double yhat, SVECT *nd) |
| |
|
double | get_quadrilateral_linear_djac_gradPhi (double xhat, double yhat, SVECT *nd, SVECT *grad_shp) |
| |
| void | integrate_quadrilateral_gradPhi_dot_Dv (SVECT *nd, SQUAD *quad, double c, STENSOR2DAI T, SVECT2D *v, double *integral_x, double *integral_y) |
| | Peforms following quadrilateral integration: More...
|
| |
| void | integrate_quadrilateral_phi_f_g (SVECT *nd, double c, double *f, double *g, double *integral) |
| | Peforms following quadrilateral integration: 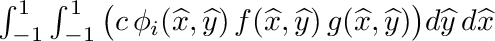 . More... . More...
|
| |
| void | integrate_quadrilateral_dphi_f_f (SVECT *nd, double c, double *f, double *integral_x, double *integral_y) |
| | Peforms following quadrilateral integration: More...
|
| |
| void | integrate_quadrilateral_dphi_f_h_h (SVECT *nd, double c, double *f, double *h, double *integral_x, double *integral_y) |
| | Peforms following quadrilateral integration: More...
|
| |
| void | integrate_quadrilateral_phi_h_g_df (SVECT *nd, double c, double *df, double *h, double *g, double *integral_x, double *integral_y) |
| | Peforms following quadrilateral integration: More...
|
| |
| void | integrate_quadrilateral_gradPhi_dot_vbar (SVECT *nd, double c, SVECT2D vbar, double *integral) |
| | Peforms following quadrilateral integration: 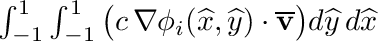 . More... . More...
|
| |
| void | integrate_quadrilateral_phi_h_df (SVECT *nd, double c, double *df, double *h, double *integral_x, double *integral_y) |
| | Peforms following quadrilateral integration: More...
|
| |
| double | integrate_quadZ_f (SVECT *nd, double c, double *f) |
| | Peforms following *vertical quadrilateral integration: 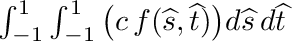 . More... . More...
|
| |
This file collections functions responsible for the 2D FE integrations


![]()
![]()
![]() .
. 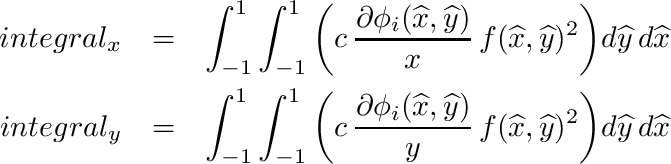
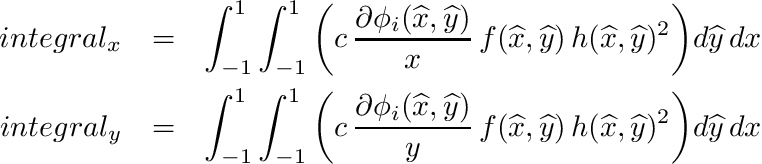
![]() .
. 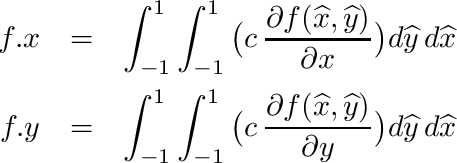
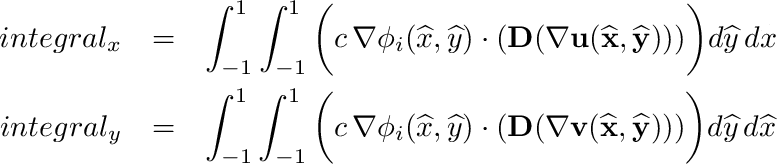
![]()
![]()
![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. 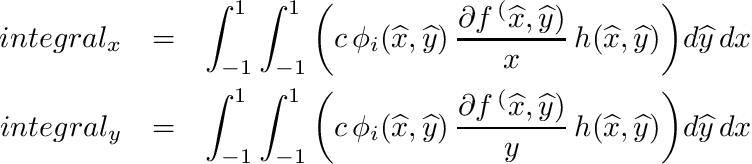
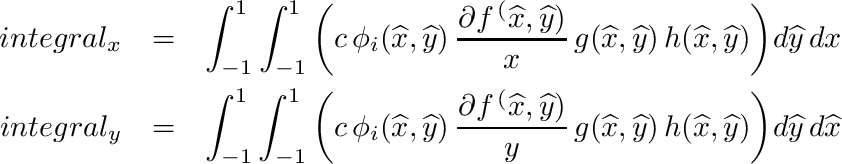
![]() .
. 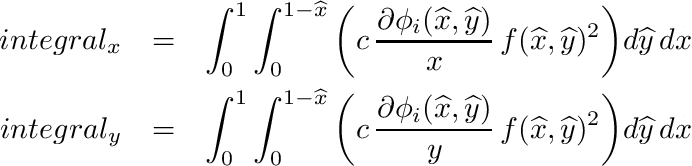
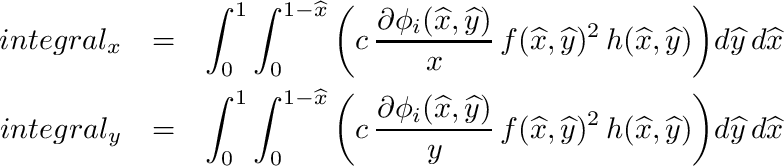
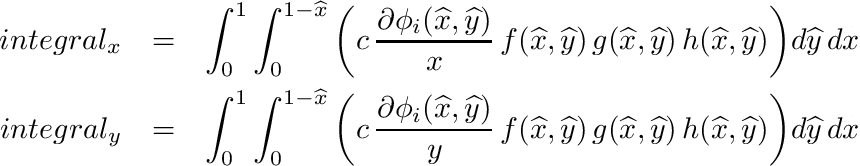
![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
. ![]() .
.